Netālās pilsētas

Stāsts
Kādā valstī atrodas pilsētas, kuras savā starpā saista ātrgaitas ceļi. Katrs ceļš ir divvirzienu un savieno divas pilsētas. Ārpus pilsētām ceļi nekrustojas.
Viena no pilsētām ir valsts galvaspilsēta un šajā uzdevumā interesēsimies par patvaļīgi izvēlētās pilsētas attālumu līdz galvaspilsētai. Uzskatīsim, ka kāda pilsēta atrodas netālu no galvaspilsētas, ja no tās iespējams aizbraukt līdz galvaspilsētai, izbraucot cauri ne vairāk kā citām pilsētām.
Vienas pilsētas un ceļu izvietojuma piemērs attēlots 1. attēlā. Pilsētas sanomērētas ar skaitļiem no līdz pēc kārtas un attēlotas ar aplīšiem, bet ceļi - kā līniju nogriežņi, kas šos aplīšus savieno. Šajā piemērā galvaspilsēta ir 7. pilsēta.
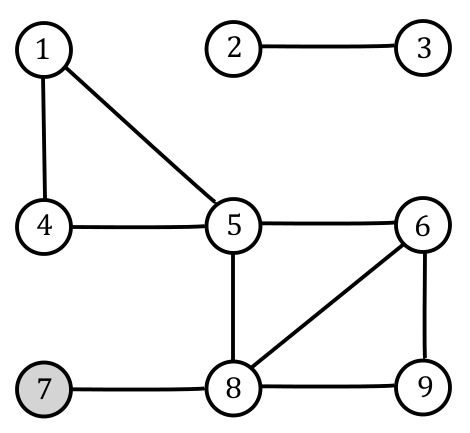
Šajā piemērā, ja , tad netālās pilsētas ir , , , un , bet visas pārējās tādas nav.
Uzrakstiet programmu, kas norādītajai pilsētas numuram nosaka, vai šī pilsēta atrodas netālu no galvaspilsētas!
Ievaddati
Ievaddatu pirmajā rindā dotas piecu veselu nenegatīvu skaitļu (), (ceļu skaits, ), (galvaspilsētas numurs, ), (pārbaudāmo pilsēju skaits, ) un (maksimālais pilsētu, kurām drīkst izbraukt cauri, skaits, ) vērtības. Nākamajās rindās dots ceļu apraksts: divi atšķirīgi naturāli skaitļi, kas norāda ceļa galos esošo pilsētas numurus. Ievaddatu pēdējā rindā doti atšķirīgi naturāli skaitļi - pārbaudāmo pilsētu numuri. Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada veseli skaitļi. Katram () -tajam skaitlim jābūt , ja ievaddatos pēc kārtas -tā pārbaudāmā pilsēta atrodas netālu no galvaspilsētas, vai - pretējā gadījumā.
Piemēri
Ievaddati
9 10 7 5 1
1 4
3 2
5 1
6 5
4 5
7 8
6 8
6 9
8 5
9 8
5 7 1 3 8
Izvaddati
1 1 0 0 1
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma formulējumā dotais tests | 2 |
| 2. | 23 | |
| 3. | 24 | |
| 4. | No katras pilsētas var nokļūt uz katru citu, turklāt tikai vienā vienīgā veidā | 25 |
| 5. | Bez papildu ierobežojumiem | 26 |
1. apakšuzdevuma ievaddati
6 10 2 6 0
5 1
5 4
5 3
1 4
1 3
1 6
1 2
4 3
3 6
6 2
1 6 4 2 3 5

Netālās pilsētas

Stāsts
Kādā valstī atrodas pilsētas, kuras savā starpā saista ātrgaitas ceļi. Katrs ceļš ir divvirzienu un savieno divas pilsētas. Ārpus pilsētām ceļi nekrustojas.
Viena no pilsētām ir valsts galvaspilsēta un šajā uzdevumā interesēsimies par patvaļīgi izvēlētās pilsētas attālumu līdz galvaspilsētai. Uzskatīsim, ka kāda pilsēta atrodas netālu no galvaspilsētas, ja no tās iespējams aizbraukt līdz galvaspilsētai, izbraucot cauri ne vairāk kā citām pilsētām.
Vienas pilsētas un ceļu izvietojuma piemērs attēlots 1. attēlā. Pilsētas sanomērētas ar skaitļiem no līdz pēc kārtas un attēlotas ar aplīšiem, bet ceļi - kā līniju nogriežņi, kas šos aplīšus savieno. Šajā piemērā galvaspilsēta ir 7. pilsēta.

Šajā piemērā, ja , tad netālās pilsētas ir , , , un , bet visas pārējās tādas nav.
Uzrakstiet programmu, kas norādītajai pilsētas numuram nosaka, vai šī pilsēta atrodas netālu no galvaspilsētas!
Ievaddati
Ievaddatu pirmajā rindā dotas piecu veselu nenegatīvu skaitļu (), (ceļu skaits, ), (galvaspilsētas numurs, ), (pārbaudāmo pilsēju skaits, ) un (maksimālais pilsētu, kurām drīkst izbraukt cauri, skaits, ) vērtības. Nākamajās rindās dots ceļu apraksts: divi atšķirīgi naturāli skaitļi, kas norāda ceļa galos esošo pilsētas numurus. Ievaddatu pēdējā rindā doti atšķirīgi naturāli skaitļi - pārbaudāmo pilsētu numuri. Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada veseli skaitļi. Katram () -tajam skaitlim jābūt , ja ievaddatos pēc kārtas -tā pārbaudāmā pilsēta atrodas netālu no galvaspilsētas, vai - pretējā gadījumā.
Piemēri
Ievaddati
9 10 7 5 1
1 4
3 2
5 1
6 5
4 5
7 8
6 8
6 9
8 5
9 8
5 7 1 3 8
Izvaddati
1 1 0 0 1
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma formulējumā dotais tests | 2 |
| 2. | 23 | |
| 3. | 24 | |
| 4. | No katras pilsētas var nokļūt uz katru citu, turklāt tikai vienā vienīgā veidā | 25 |
| 5. | Bez papildu ierobežojumiem | 26 |
1. apakšuzdevuma ievaddati
6 10 2 6 0
5 1
5 4
5 3
1 4
1 3
1 6
1 2
4 3
3 6
6 2
1 6 4 2 3 5