A + B
Krišjānim patīk skaitļi. Viņš uzskata, ka skaitļi ir ļoti svarīgi, un viņš tos lieto visur. Taču viņš nemāk skaitīt. Viņam neizdodas izrēķināt, cik ir . Palīdziet Krišjānim, uzrakstot programmu, kas aprēķina šo divu skaitļu summu!
Receptes
Slavenais konditors Mārtiņš Vakariņš ir savācis lielu toršu recepšu kolekciju. Pēdējā laikā Vakariņš ir pamanījis, ka ir grūti atcerēties vai atrast noteiktas tortes recepti, tādēļ ir izveidojis datorsistēmu, kurā ievadījis visas zināmās receptes, katrai no tortēm norādot nepieciešamo izejvielu daudzumu kā veselu nenegatīvu skaitļu virkni . Katram () norāda -tās sastāvdaļas daudzumu noteiktās vienībās (piemēram, cukura vai miltu mērvienība būs izteikta gramos, olu dzeltenumi gabalos, utt.). Ja konkrētai receptei attiecīgā sastāvdaļa nav


Bulciņas un vēlmes
Slavena beķereja katru rītu izcep bulciņas (ar tām saprotot arī kūciņas un smalkmaizītes), un visas tās pirms beķerejas atvēršanas izvieto vitrīnā. Tad beķereja tiek atvērta un pēc kārtas tiek apkalpoti pircēji. Katrs pircējs vēlas nopirkt vienu bulciņu un uzskatīsim, ka katram pircējam ir tieši trīs visiecienītākie bulciņu veidi jeb prioritātes. Ir iespējams, ka kādam pircējam vairākas prioritātes sakrīt, kā arī var būt, ka starp prioritātēm ir tādi bulciņu veidi, kurus slavenā beķereja nemaz nepiedāvā. Katrs pircējs rīkojas pēc šāda algoritma: - JA ir pieejama 1. prioritātes

Daļu salīdzināšana
Salīdzini divas daļas, lai noteiktu, kura no tām ir lielāka vai ja tās ir vienādas. Jums ir jāizstrādā datorprogramma, kas ņem vērā ievadītos četrus veselos skaitļus , , un , lai salīdzinātu daļas un .

Dažādie skaitļi
Naturālu skaitļu virknē nepieciešams atrast garāko fragmentu (secīgu elementu virkni), kur visi skaitļi būtu atšķirīgi. Piemēram, virknē garākais fragments, kur visi skaitļi ir atšķirīgi, ir garumā un sākas ar trešo elementu: . Uzrakstiet datorprogrammu, kas dotai skaitļu virknei atrod garākā fragmenta, kurā visi skaitļi ir atšķirīgi, garumu un visas šādu fragmentu atrašanās vietas!


Siers
Pelēns Lio ir atradis milzīgu siera šķēli, ko var raksturot kā rūtiņu laukumu ar rindām un kolonnām. Siera šķēles rūtiņu -tajā rindā un -tajā kolonnā var aprakstīt ar veselu skaitli - tā garšīgumu. Kādas siera rūtiņas var būt sapelējušas -- šādu rūtiņu garšīgums tiek uzdots kā negatīvs skaitlis. Lio vēlas šo sieru ēst pēc sekojošiem noteikumiem: - katrā rindā jāapēd vismaz viena rūtiņa; - nevienā rindā nedrīkst apēst visas rūtiņas; - tieši rindās viņam siers jāēd sākot no kreisās puses (pēc kārtas rūtiņas ar indeksiem ), pārējās rindās viņam si

A+B=C
Dotas kartītes. Uz katras kartītes uzrakstīts kāds vesels skaitlis. Uz vairākām kartītēm var būt uzrakstīti vienādi skaitļi. Nepieciešams noteikt, vai no dotajām iespējams izvēlēties trīs atšķirīgas kartītes (nosauksim tās par , un ), ka uz kartītēm un uzrakstīto skaitļu summa ir vienāda ar uz kartītes uzrakstīto skaitli. Piemēram, no skaitļiem kā , un var izvēlēties kartītes ar uz tām uzrakstītiem skaitļiem () vai (). Uzrakstiet datorprogrammu, kas atrod šādu kartīšu trijnieku, vai arī nosaka, ka

Gūtie punkti
Mums nepazīstamas sporta spēles turnīrā piedalās dalībnieki, kas sanumurēti pēc kārtas ar naturāliem skaitļiem no līdz . Turnīra sākumā visiem spēlētājiem ir nulle punktu. Tiek izspēlētas spēles, kur katrā kādi divi spēlētāji tiekas savā starpā, un ir zināmi spēļu rezultāti to notikšanas secībā. Katra spēle ir ar punktu summu – viens spēlētājs iegūst punktus, bet otrais zaudē punktus. Turnīra beigās jāatbild uz vaicājumiem. Ir iespējami četri vaicājumu veidi: 1. Cik punktu turnīra beigās ir ieguvis dalībnieks ? 2. Cik reižu turnīra laikā dalībnieks ir sa


Hokeja turnīrs
No turnīra tabulas žurnālisti vēlas uzzināt komandu uzvaru secību. Dotajā tabulā spēle turpinās līdz vienas komandas uzvarai, un visas komandas ir sanumurētas ar naturāliem skaitļiem no 1 līdz . Pēc turnīra beigām nepieciešams izvietot visas komandas tā, ka katra komanda uzvar nākamo. Pieņemsim, ka turnīrā piedalās piecas komandas un sākotnējā tabula ir, kā redzams attēlā (kur -tās rindas -tajā kolonnā ierakstīts 1, ja uzvarēja -tā komanda, bet 0, ja -tā komanda). Iespējama komandu secība ir . Šī nav vienīgā iespējamā.

Izsmalcinātās kūkas
Izsmalcinātais ēdiena kritiķis Valters ir ieradies īpaši izsmalcinātā beķerejā. Beķeris viņam priekšā noliek kūkas secīgi rindā, kur -tās kūkas garšīgums ir un tās tips ir . Valters pussekundi pēc kūku ieraudzīšanas pavēstīja, ka savā pasūtījumā vēlas daudzveidību, tāpēc ir gatavs nogaršot tikai tādus kūku komplektus, kur katrām divām kūkām to tipu vērtības atšķiras par vismaz (formāli, katrām divām paņemtajām kūkām () jāizpildās ). Beķeris grib atstāt labu iespaidu uz ēdiena kritiķi Valteru, tāpēc no visām kūkām izvēlēsies tādu komp


Kvadrātveida putekļsūcējs
Krišjānis ir uzkonstruējis kvadrātveida putekļsūcēju (saīsināti – KP), kas ir neaizstājams palīgs viņa darbnīcas uzkopšanā. KP atmiņā darbnīcas grīda tiek attēlota kā rūtiņu laukums, kurā pats KP aizņem rūtiņas. Laukumā dažas rūtiņas var būt bīstamas (netērēsim laiku, mēģinot noskaidrot, ko tieši tas nozīmē), un KP nekad nedrīkst nonākt situācijā, ka KP atrašanās vietā vairāk nekā puse tā noklāto rūtiņu ir bīstamas. Ir zināma KP sākotnējā atrašanās vieta un īpaša rūtiņa, kura noteikti jāuzkopj, t.i., KP jāuzbrauc uz tās. Vienā solī KP var pārvietoties par vienu rūtiņu

Perfekts labirints
Tavs draugs veido labirintus, un viņa mērķis ir izveidot perfektu labirintu. Tā kā šāda labirinta izveide nebūt nav vienkārša, viņš lūdz Tavu palīdzību. Ir zināms, ka perfekts labirints atbilst šādiem nosacījumiem: - Labirints ir rūtiņu laukums ar rindām (numurētas virzienā no augšas uz leju ar naturāliem skaitļiem pēc kārtas no līdz ) un kolonnām (numurētas no kreisās uz labo pusi ar naturāliem skaitļiem pēc kārtas no līdz ). Rūtiņa ar koordinātām atbilst rūtiņai laukuma kolonnā un rindā. - Katra rūtiņa ir vai nu tukša (caur to var iziet) vai _aizp


Monētas
Kasieris Naudiņš katru naudas summu vēlas izsniegt, izmantojot pieejamo nominālu monētas tā, ka kopējais monētu skaits ir mazākais iespējamais. Var uzskatīt, ka katra nomināla monētas Naudiņam ir pieejamas neierobežotā skaitā. Piemēram, ja un pieejamas trīs veidu monētas, kuru nomināli ir un vienības, tad nepieciešamo naudas summu var izveidot ar divu monētu palīdzību: vai . Savukārt, izmantojot tikai šī veida monētas, nav iespējams izveidot naudas summas, kuru vērtība ir vai . Uzrakstiet programmu, kas dotai vērtībai un monētu nomināliem at

Netālās pilsētas
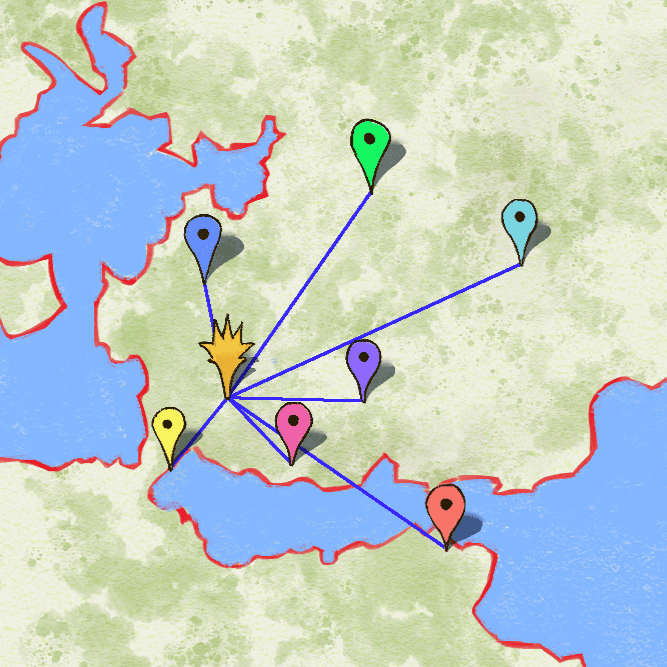
Kādā valstī atrodas pilsētas, kuras savā starpā saista ātrgaitas ceļi. Katrs ceļš ir divvirzienu un savieno divas pilsētas. Ārpus pilsētām ceļi nekrustojas. Viena no pilsētām ir valsts galvaspilsēta un šajā uzdevumā interesēsimies par patvaļīgi izvēlētās pilsētas attālumu līdz galvaspilsētai. Uzskatīsim, ka kāda pilsēta atrodas netālu no galvaspilsētas, ja no tās iespējams aizbraukt līdz galvaspilsētai, izbraucot cauri ne vairāk kā citām pilsētām. Vienas pilsētas un ceļu izvietojuma piemērs attēlots 1. attēlā. Pilsētas sanomērētas ar skaitļiem no līdz pēc kārtas un attēl


Otrais ceļojums
Tūristu iecienītajā Krokodilu salā ir pilsētas, kas numurētas ar naturāliem skaitļiem no līdz pēc kārtas. Visas pilsētas savā starpā savieno ceļu tīkls. Ceļi ir izbūvēti tā, ka no katras pilsētas uz jebkuru citu iespējams aizbraukt pa ceļiem tikai vienā vienīgā veidā. Tūristu ērtībām katrā salas pilsētā ir lidosta, kurā tūristi var sākt un beigt savus ceļojumus. Ceļojumu aģentūra „Jaunie skati” piedāvā organizēt ceļojumus uz Krokodilu salu, kuri noris šādi: vispirms tūrists ar lidmašīnu tiek aizvests uz kādu no Krokodilu salas pilsētām (apzīmēsim to ar ), pēc tam, vadoties no tū


Beķerejas vitrīna
Slavena beķereja katru rītu noteiktā secībā izcep bulciņas (ar tām saprotot arī kūciņas un smalkmaizītes), un tās pirms beķerejas atvēršanas to izcepšanas secībā izvieto vitrīnā. Diemžēl, vitrīnā ir vieta tikai bulciņām, tāpēc pēc kārtas nākamā bulciņa tajā tiek novietota tikai tad, kad kāda no vitrīnā izliktajām bulciņām tiek nopirkta un tās aizņemtā vieta atbrīvojas. Tad beķereja tiek atvērta un pēc kārtas tiek apkalpoti pircēji. Katrs pircējs vēlas nopirkt vienu bulciņu un uzskatīsim, ka katram pircējam ir tieši trīs visiecienītākie bulciņu veidi jeb prioritātes. Ir iespējams

Atklātās rūtiņas
Pēteris ir izdomājis jaunu datorspēli, kas notiek uz liela rūtiņu laukuma un kurā darbojas viens vai vairāki tēli. Katrs tēls atrodas kādā no laukuma rūtiņām. Vienā laukuma rūtiņā var atrasties vairāki tēli. Spēlētājam ir atklātas(redzamas) tikai tās rūtiņas, kuras atrodas netālu no kāda tēla, bet pārējās ir aizklātas(slēptas). Precīzāk - dotam skaitlim spēlētājam ir redzamas tikai laukuma rūtiņas ar koordinātām , kurās atrodas tēli, un visas rūtiņas, kuru koordinātām vienlaikus ir spēkā sakarības un . 1\

Bojātais kabelis
Kādā datorfirmā datori ir saslēgti vienotā tīklā tā, ka katru divu datoru pāris ir vai nu tieši savienots ar kabeli, vai arī eksistē unikāla secīgu datoru virkne no viena datora līdz otram, kur katrus divus blakus datorus savieno kabelis. Datori tīklā ir sanumurēti ar naturāliem skaitļiem no līdz pēc kārtas. Viena šāda datortīkla piemērs parādīts 1. attēlā. Meistars Matīss ir pamanījis, ka datortīkls vairs nedarbojas kā nākas, un pēc viņa ilggadējās iepriekšējās pieredzes ir skaidrs, ka vainīgs ir kāds no si

Divi pāri
Dotas kartītes. Uz katras kartītes uzrakstīts kāds vesels skaitlis. Uz vairākām kartītēm var būt uzrakstīti vienādi skaitļi. Nepieciešams noteikt, vai no dotajām iespējams izvēlēties četras atšķirīgas kartītes (nosauksim tās par , , un ), ka uz kartītēm un uzrakstīto skaitļu summa ir vienāda ar uz kartītēm un uzrakstīto skaitļu summu. Piemēram, no skaitļiem , , , , , kā , , un var izvēlēties kartītes ar uz tām uzrakstītajiem skaitļiem , , , (). Uzrakstiet datorprogrammu, kas atrod šādu kartīšu

Dīvainā kārtošana
Aplūkosim šādu visai dīvainu naturālu skaitļu kārtošanas algoritmu: No dotajiem skaitļiem izvēlas mazāko skaitli - tas sakārtotajā virknē būs pirmais loceklis . No atlikušajiem skaitļiem izvēlas mazāko skaitli, kura ciparu summa ir lielāka par ciparu summu - tas sakārtotajā virknē būs otrais loceklis . No atlikušajiem skaitļiem izvēlas mazāko skaitli, kas vienlaikus ir lielāks par un kura ciparu summa ir lielāka par ciparu summu. Tas būs . Tā turpina, kārtējam iegūtajam virknes loceklim no atlikušajiem skaitļiem meklējot mazāko skaitli, kurš g


Nevēlamā konfekšu kaste
"Mazās konfekšu darbnīcas" noliktavā ir () dažādas ietilpības kastes veidi. Katra veida kastē var ielikt attiecīgi konfektes. Var uzskatīt, ka katra veida kastes noliktavā ir neierobežotā skaitā. Galvenais tehnologs Tālis nekad iepriekš nezin, kura viena veida kastes viņam šodien tiks padotas, tāpēc viņam jābūt gatavam pilnībā piepildīt jebkura veida kastes tā, lai neviena konfekte nepaliktu pāri. Tālis, zinot visu kastu veidu ietilpību, katru dienu izgatavo mazāko nepieciešamo konfekšu skaitu . Piemēram, ja noliktavā ir piecu veidu kastes, kuru ietilpība


Patiesības teicēji un meļi
Kādā ciemā dzīvo iedzīvotāji, kas sanumurēti ar naturāliem skaitļiem no līdz pēc kārtas. Katrs ciemata iedzīvotājs ir vai nu patiesības teicējs, kas vienmēr saka taisnību, vai arī melis, kas visu laiku melo. Etnogrāfam Rihardam ir izdevies savākt ciema iedzīvotāju izteikumus vienam par otru. Visus izteikumus Rihards ir pierakstījis formā: - "Ciema iedzīvotājs apgalvo, ka iedzīvotājs ir patiesības teicējs." vai - "Ciema iedzīvotājs apgalvo, ka iedzīvotājs ir melis." Šajos apgalvojumos un . Rihards vēlas noskaidrot, kāds

Tramvaju vērošana
Pieturā pietur maršrutu tramvaji. Mazajam Arnoldam patīk vērot tramvajus un pierakstīt pienākošo tramvaju numurus. Šobrīd viņš ir pierakstījis ciparu virkni - tramvaju numuru virkni bez atdalītājiem. Nepieciešams noteikt lielāko iespējamo Arnolda novēroto katra maršruta tramvaju skaitu. Piemēram, ja pieturā pietur , un maršruta tramvaji un Arnolda pierakstītā ciparu virkne ir , tad un maršruta tramvajs varēja būt pienācis, augstākais, divas reizes, bet maršruta tramvajs - vienu. Ievērojiet, ka ciparu virknē parādās trīsreiz, bet kore


Uzmini skaitli!
Dators "ir iedomājies" naturālu skaitli robežās no līdz . Skaitļa atminēšanai Jūsu programma var veikt vaicājumus. Katrs vaicājums ir formā "Vai iedomātais skaitlis ir ?", kur , un uz katru šādu vaicājumu dators dod vienu no trim atbildēm: - , ja , - , ja , - , ja . Skaitlis ir uzminēts tikai tad, ja ir izdarīts vaicājums uz kuru saņemta atbilde . Katram vaicājumam ir noteikta maksa – ja vaicājumā izmatots skaitlis , tad maksa par šādu vaicājumu ir eirocenti. Uzrakstiet datorprogrammu, kas atrod skaitli $

Zāģa starpība
Naturālu skaitļu virkni sauksim par zāģa virkni, ja tās locekļus saista sakarība: Piemēram, zāģa virknes ir 7, 8, 4, 13, 4 un 7, 13, 4, 8, 4, bet nav – 4, 4, 13, 8, 7 un 13, 4, 8, 4, 7. Ja zāģa virknē ir vairāk par vienu elementu, tad šādai virknei varam aprēķināt katru divu blakus skaitļu starpību pēc moduļa un tad atrast mazāko no šīm starpībām. Piemēram, ja doti skaitļi 1, 2, 4, 4, 7, 7, 9, 11, 12, tad no tiem var izveidot vairākas zāģa virknes ar atšķirīgu mazāko blakus skaitļu starpību pēc moduļa: - 11-12-7-9-4-7-2-4-1 (

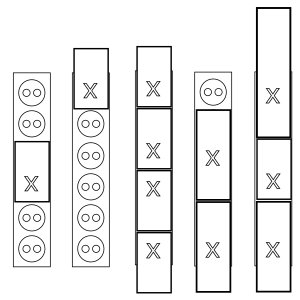
Adapteru rinda
Mūsdienu elektroniskajām iekārtām ir nepieciešama regulāra uzlāde, kas parasti tiek veikta, izmantojot dažādu izmēru adapterus. Šajā uzdevumā interesēsimies par adapteru ieslēgšanu kontaktligzdu blokā, kur kontaktligzdas izvietotas vienā rindā (1. attēlā (a) parādīts sešu kontaktligzdu bloks). Katra adaptera kontaktdakšiņa ir novietota tā, ka, ieslēdzot to kontaktligzdā, adaptera garākā mala būs paralēla kontaktligzdu bloka garākajai malai, turklāt kontaktligzdā adapteru var ieslēgt divos variantos – viens variants no otra atšķiras ar pagriešanu par grādiem. Pieņemsim, ka katra adaptera

Dārgākais posms
Loģistika ir zinātne par to, kā jebkuras sistēmas ietvaros objektīvāk plānot, regulēt un kontrolēt informācijas, materiālu, produkcijas, cilvēku un enerģijas plūsmas, kā arī visaptveroša šo plūsmu vadīšana; ar ražojumu izplatīšanu saistīto darbu optimizēšana. Pētnieks Konrāds šobrīd analizē kādas transporta firmas materiālu pārvadāšanas plūsmas. Viņš ir noskaidrojis, ka firma savus pārvadājumus veic tikai starp noteiktām pilsētām tā, ka katrs posms saista tieši divas pilsētas, turklāt pārvadājums no vienas pilsētas līdz kādai citai vienmēr ir šādu posmu virkne, kas vienmēr iespējama tikai vie

Vienvirziena ielas
Kādā pilsētā visas ielas ir vienvirziena un katra no tām ir vērsta vai nu ziemeļu (kartē vertikāli uz augšu), vai dienvidu (kartē vertikāli uz leju), vai rietumu (kartē horizontāli pa kreisi), vai austrumu (kartē horizontāli pa labi) virzienā (skat. 1. attēlu). Kopumā ielas ir vērstas ziemeļu vai dienvidu virzienā, bet ielas — austrumu vai rietumu virzienā. Ziemeļu/dienvidu ielas ir sanumurētas ar naturāliem skaitļiem no līdz pēc kārtas, sākot no kreisās puses uz labo, bet rietumu/austrumu ielas ir sanumurētas ar naturāliem skaitļiem no līdz pēc kārtas, sākot no augšas


Svītraino paklāju summas
Valtera mājās ir zemāk redzamais paklājs, par kura rakstu varētu teikt, ka tas sastāv no "koncentriskiem rūtiņu taisnstūriem". Skatoties uz paklāja rakstu, Valters ir izdomājis, ka šim paklāja rakstam līdzīgu šablonu varētu izmantot skaitļu tabulā, summējot tajā ierakstītos skaitļus noteiktā veidā. Precīzāk - aplūkojam taisnstūra rūtiņu laukumus, kur katrā rūtiņā ir ierakstīts kāds vesels skaitlis. Laukuma rindas un kolonnas numurētas ar naturāliem skaitļiem pēc kārtas, sākot no . Tad izvēlamies rūtiņu laukumā kādu apakštaisnstūri un tam aprēķinām "s

Paralelogrami
Šajā uzdevumā aplūkosim paralelogramus, kuru virsotnes atrodas Dekarta koordinātu plaknē punktos ar veselām koordinātām. Atkarībā no paralelograma virsotņu novietojuma, arī tā diagonāļu krustpunkts var atrasties punktā ar veselām koordinātām. Piemēram, ja paralelograma virsotnes atrodas punktos ar koordinātām , , un , tad tā diagonāļu krustpunkts atrodas punktā ar koordinātām . Uzrakstiet datorprogrammu, kas nosaka, cik dažādos veidos no dotajiem punktiem ar veselām koordinātām var izvēlēties četrus punktus tā, ka šī paralelograma diagonāles krustoj

Pētera bumbiņas
Pēteris tagad spēlē Riharda izdomāto divdimensiju datorspēli, kurā tiek imitēta bumbiņu nokrišana uz horizontālas virsmas. Virsma tiek attēlota kā horizontāla līnija ar sanumurētām pozīcijām vienas bumbiņas platumā. Pozīciju ir bezgalīgi daudz un tās numurētas ar veseliem skaitļiem, sākot no nulles uz abām pusēm. Sākumā virsma ir tukša. Kādā pozīcijā no augšas viena pēc otras tiek nomestas bumbiņas. Ja bumbiņa nokrīt uz virsmas, tad tā paliek tajā pozīcijā, kurā tā tobrīd atrodas. Ja bumbiņa nonāk pozīcijā ar numuru , kurā jau atrodas kāda bumbiņa, tad tā tālāk pārvietojas pēc šādiem noteik


Seifs
Inženieris Žeņa veido izsmalcinātu elektroniski-mehānisku seifa atslēgu, kura sastāv no apļveida korpusa ar kontaktiem un grozāma koncentriska regulāra -stūra tā iekšpusē. Katra daudzstūra virsotne arī ir kontakts. Sākotnēji katra regulārā daudzstūra virsotne atrodas pretī kādam no korpusa kontaktiem. Iekšējais daudzstūris ir grozāms, bet tikai par konstantu soli - veselu skaitu iedaļu. Tādējādi, iekšējā daudzstūra virsotnes arī pēc pagriešanas vienmēr atrodas pretī korpusa kontaktiem. Vienam vai vairākiem korpusa kontaktiem ir pievienoti sarkani vadi, kas tos savieno ar citām elektron


Tornis II
Uz bezgalīgas rūtiņu lapas, kurai dažas rūtiņas var būt izgrieztas, novietota šaha figūra - tornis. Lapas rindas un kolonnas ir sanumurētas pēc kārtas ar veseliem skaitļiem. Kolonnas ir numurētas no kreisās puses uz labo, bet rindas - no lejas uz augšu. Tornis vienā gājienā var pārvietoties uz jebkuru citu neizgrieztu lapas rūtiņu, kas ar sākotnējā atrodas vienā rindā vai kolonnā. Tornis nedrīkst pārvietoties pāri izgrieztai rūtiņai. Laukuma piemērā 1. attēlā redzams, uz kurām rūtiņām tornis drīkst pārvietoties, ja četras lapas rūtiņas ir izgrieztas un tornis pirms gājiena atrodas rūtiņā ar ko
