Pētera bumbiņas

Stāsts
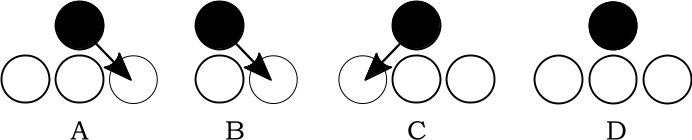
Pēteris tagad spēlē Riharda izdomāto divdimensiju datorspēli, kurā tiek imitēta bumbiņu nokrišana uz horizontālas virsmas. Virsma tiek attēlota kā horizontāla līnija ar sanumurētām pozīcijām vienas bumbiņas platumā. Pozīciju ir bezgalīgi daudz un tās numurētas ar veseliem skaitļiem, sākot no nulles uz abām pusēm. Sākumā virsma ir tukša. Kādā pozīcijā no augšas viena pēc otras tiek nomestas bumbiņas. Ja bumbiņa nokrīt uz virsmas, tad tā paliek tajā pozīcijā, kurā tā tobrīd atrodas. Ja bumbiņa nonāk pozīcijā ar numuru , kurā jau atrodas kāda bumbiņa, tad tā tālāk pārvietojas pēc šādiem noteikumiem (skat. 1. att.):
-
ja pozīcijā pa labi (numurs ) blakus tieši zem esošajai bumbiņai ir brīva vieta, tad bumbiņa pārvietojas uz to (1. att. A vai B);
-
ja pozīcija pa labi (numurs ) blakus tieši zem esošās bumbiņas ir aizņemta, bet pozīcija pa kreisi (numurs ) ir brīva, tad bumbiņa pārvietojas uz to (1. att. C);
-
ja abas kaimiņu pozīcijas tieši zem esošās bumbiņas ir aizņemtas, tad bumbiņa paliek pozīcijā (1. att. D).
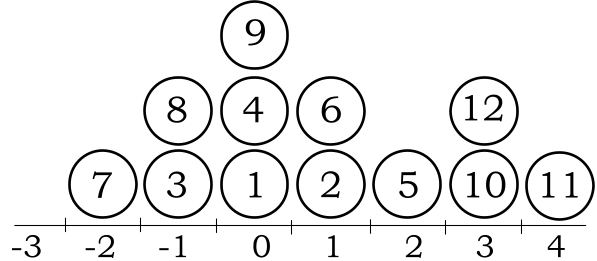
Bumbiņa jaunajā pozīcijā pārvietojas pēc aprakstītajiem likumiem, līdz kamēr apstājas. Ja vispirms deviņas bumbiņas nomet pozīcijā 0 un tad trīs bumbiņas pozīcijā 3, tad iegūst tādu bumbiņu izvietojumu kā parādīts 2. attēlā.
Uzrakstiet datorprogrammu, kas dotam bumbiņu mešanas aprakstam nosaka, kur pēc katras nomešanas reizes apstāsies pēdējā nomestā bumbiņa!
Ievaddati
Ievaddatu pirmajā rindā dota naturāla skaitļa (bumbiņu mešanas reižu skaits, ) vērtība. Nākamajās rindās aprakstīta bumbiņu mešana. Katram ievaddatu -ajā rindā doti divi veseli skaitļi: pozīcijas numurs un tajā nomesto bumbiņu skaits . Zināms, ka nevienā testā kopējais nomesto bumbiņu skaits nepārsniedz .
Izvaddati
Izvaddatiem jāsatur tieši rindas un pēc katras mešanas reizes jāsatur informācija par pēdējās nomestās bumbiņas atrašanās vietu. Precīzāk, katram izvaddatu -tajā rindā jāizvada divi naturāli skaitļi, kas atdalīti ar tukšumzīmi – pozīcijas, kurā apstāsies pēdējā -tajā mešanas reizē nomestā bumbiņa, numurs un bumbiņu skaits pozīcijā pēc šīs bumbiņas apstāšanās.
Piemēri
Ievaddati
1
0 5
Izvaddati
2 1
Ievaddati
2
0 9
3 3
Izvaddati
0 3
3 2
Ievaddati
3
0 8
0 7
0 5
Izvaddati
-1 2
-1 3
1 4
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Trīs uzdevuma tekstā dotie testi | 2 |
| 2. | 8 | |
| 3. | , | 10 |
| 4. | , | 10 |
| 5. | , visiem | 15 |
| 6. | , visiem | 15 |
| 7. | 25 | |
| 8. | Bez papildu ierobežojumiem | 15 |
1. apakšuzdevuma ievaddati
3
-1000000 3
1000000 5
0 5
7
1607 13
2415 55
1607 11
2415 17
760194 1
-12164 1
330520 2
8
2019 8
2019 11
788 1
788 4
1689 23
2028 4
2019 6
765 43
Pētera bumbiņas

Stāsts
Pēteris tagad spēlē Riharda izdomāto divdimensiju datorspēli, kurā tiek imitēta bumbiņu nokrišana uz horizontālas virsmas. Virsma tiek attēlota kā horizontāla līnija ar sanumurētām pozīcijām vienas bumbiņas platumā. Pozīciju ir bezgalīgi daudz un tās numurētas ar veseliem skaitļiem, sākot no nulles uz abām pusēm. Sākumā virsma ir tukša. Kādā pozīcijā no augšas viena pēc otras tiek nomestas bumbiņas. Ja bumbiņa nokrīt uz virsmas, tad tā paliek tajā pozīcijā, kurā tā tobrīd atrodas. Ja bumbiņa nonāk pozīcijā ar numuru , kurā jau atrodas kāda bumbiņa, tad tā tālāk pārvietojas pēc šādiem noteikumiem (skat. 1. att.):
-
ja pozīcijā pa labi (numurs ) blakus tieši zem esošajai bumbiņai ir brīva vieta, tad bumbiņa pārvietojas uz to (1. att. A vai B);
-
ja pozīcija pa labi (numurs ) blakus tieši zem esošās bumbiņas ir aizņemta, bet pozīcija pa kreisi (numurs ) ir brīva, tad bumbiņa pārvietojas uz to (1. att. C);
-
ja abas kaimiņu pozīcijas tieši zem esošās bumbiņas ir aizņemtas, tad bumbiņa paliek pozīcijā (1. att. D).
Bumbiņa jaunajā pozīcijā pārvietojas pēc aprakstītajiem likumiem, līdz kamēr apstājas. Ja vispirms deviņas bumbiņas nomet pozīcijā 0 un tad trīs bumbiņas pozīcijā 3, tad iegūst tādu bumbiņu izvietojumu kā parādīts 2. attēlā.


Uzrakstiet datorprogrammu, kas dotam bumbiņu mešanas aprakstam nosaka, kur pēc katras nomešanas reizes apstāsies pēdējā nomestā bumbiņa!
Ievaddati
Ievaddatu pirmajā rindā dota naturāla skaitļa (bumbiņu mešanas reižu skaits, ) vērtība. Nākamajās rindās aprakstīta bumbiņu mešana. Katram ievaddatu -ajā rindā doti divi veseli skaitļi: pozīcijas numurs un tajā nomesto bumbiņu skaits . Zināms, ka nevienā testā kopējais nomesto bumbiņu skaits nepārsniedz .
Izvaddati
Izvaddatiem jāsatur tieši rindas un pēc katras mešanas reizes jāsatur informācija par pēdējās nomestās bumbiņas atrašanās vietu. Precīzāk, katram izvaddatu -tajā rindā jāizvada divi naturāli skaitļi, kas atdalīti ar tukšumzīmi – pozīcijas, kurā apstāsies pēdējā -tajā mešanas reizē nomestā bumbiņa, numurs un bumbiņu skaits pozīcijā pēc šīs bumbiņas apstāšanās.
Piemēri
Ievaddati
1
0 5
Izvaddati
2 1
Ievaddati
2
0 9
3 3
Izvaddati
0 3
3 2
Ievaddati
3
0 8
0 7
0 5
Izvaddati
-1 2
-1 3
1 4
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Trīs uzdevuma tekstā dotie testi | 2 |
| 2. | 8 | |
| 3. | , | 10 |
| 4. | , | 10 |
| 5. | , visiem | 15 |
| 6. | , visiem | 15 |
| 7. | 25 | |
| 8. | Bez papildu ierobežojumiem | 15 |
1. apakšuzdevuma ievaddati
3
-1000000 3
1000000 5
0 5
7
1607 13
2415 55
1607 11
2415 17
760194 1
-12164 1
330520 2
8
2019 8
2019 11
788 1
788 4
1689 23
2028 4
2019 6
765 43