programme.lv

Svītraino paklāju summas

ļoti grūts

Uzdevums no Latvijas 38. (2024./2025. m.g.) informātikas olimpiādes (LIO) valsts kārtas; vecākajai (11.-12. klašu) grupai.

Stāsts

Valtera mājās ir zemāk redzamais paklājs, par kura rakstu varētu teikt, ka tas sastāv no "koncentriskiem rūtiņu taisnstūriem".

Skatoties uz paklāja rakstu, Valters ir izdomājis, ka šim paklāja rakstam līdzīgu šablonu varētu izmantot skaitļu tabulā, summējot tajā ierakstītos skaitļus noteiktā veidā.

Precīzāk - aplūkojam taisnstūra rūtiņu laukumus, kur katrā rūtiņā ir ierakstīts kāds vesels skaitlis. Laukuma rindas un kolonnas numurētas ar naturāliem skaitļiem pēc kārtas, sākot no $1$ . Tad izvēlamies rūtiņu laukumā kādu apakštaisnstūri un tam aprēķinām "svītrainā paklāja summu" $S$ :

sākumā $S=0$ ,
visus skaitļus, kas atrodas uz šī apakštaisnstūra ārējā kontūra, pieskaita $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, atņem no $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, pieskaita $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, atņem no $S$ ,
utt., pārmaiņus skaitļus no kārtējā kontūra vai nu pieskaita, vai atņem no $S$ .

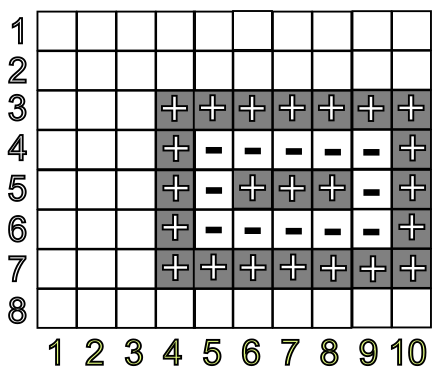
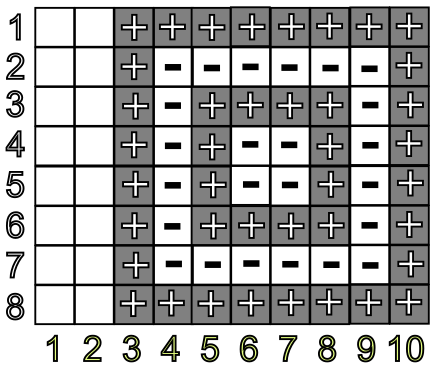
Piemēram, ja visās $10 \times 8$ laukuma rūtiņās katrā ierakstīts $1$ un izvēlēts apakštaisnstūris ar izmēru $7 \times 5$ , kura kreisais augšējais stūris atrodas rūtiņā $(4; 3)$ (2. attēls), tad šāda apakštaisnstūra svītrainā paklāja summa $S$ ir $11$ . Bet, ja šim pašam laukumam būtu izvēlēts $8 \times 8$ apakštaisnstūris, kura kreisais augšējais stūris atrodas rūtiņā $(3; 1)$ (3. attēls), tad šāda apakštaisnstūra svītrainā paklāja summa $S$ ir $16$ . Attēlos ar tumšāku krāsu iezīmēti kontūri, kuros esošie skaitļi summai tiek pieskaitīti, bet ar gaišu - kuros atņemti.

Uzrakstiet datorprogrammu, kas dotam laukuma rūtiņu aizpildījumam un apakštaisnstūru novietojuma aprakstam katram no apakštaisnstūriem aprēķina svītrainā paklāja summu!

2. attēls: Paklāja šablons 7 x 5, stūris: (4;3)

3. attēls: Paklāja šablons 8 x 8, stūris: (3;1)

Ievaddati

Pirmajā rindā doti trīs naturāli skaitļi - rūtiņu laukuma platums $N$ ( $N \leq 1000$ ), laukuma augstums $M$ ( $M \leq 1000$ ) un vaicājumu skaits $V$ ( $V \leq 2 \cdot 10^5$ ).

Nākamajās $M$ ievaddatu rindās katrā doti $N$ skaitļi - vienas laukuma rindas rūtiņās ierakstītie skaitļi. Katram $i$ ( $1 \leq i \leq M$ ) un $j$ ( $1 \leq j \leq N$ ) laukuma $i$ -tās rindas $j$ -tās kolonnas rūtiņā ierakstītais skaitlis ir dots ievaddatu $i+1$ -jā rindā kā $j$ -tais pēc kārtas. Zināms, ka visi laukuma rūtiņās ierakstītie skaitļi ir robežās no $-10^9$ līdz $10^9$ .

Nākamajās $V$ ievaddatu rindās katrā dots viena vaicājuma apraksts - apakštaisnstūra platums un augstums, kā arī apakštaisnstūra kreisā augšējā stūra rūtiņas koordinātas (tās kolonnas un rindas numurs). Zināms, ka katrs apakštaisnstūris pilnībā ietilpst dotajā laukumā.

Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.

Izvaddati

Izvaddatiem jāsatur $V$ rindas. Katram $v$ ( $1 \leq v \leq V$ ) izvaddatu $v$ -tajā rindā jāizvada vesels skaitlis - tā apakštaisnstūra, kas ievaddatos dots kā $v$ -tais pēc kārtas, svītrainā paklāja summa $S$ .

Piemēri

Ievaddati

10 8 4
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
7 5 4 3
8 8 3 1
1 2 5 5
1 1 4 2

Izvaddati

Piezīme:

Atbilst piemēram uzdevuma tekstā.

Ievaddati

10 8 4
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
7 2 4 3
1 5 7 2
1 1 6 5
10 8 1 1

Izvaddati

Izpildes resursu ierobežojumi

CPU izpildes laiks uz testu: 0.6 sekundes.

RAM atmiņas apjoms uz testu: 256 megabaiti.

Apakšuzdevumi un to vērtēšana

#	Apakšuzdevuma apraksts	Punkti
1.	Uzdevuma tekstā dotais tests	2
2.	Visos vaicājumos apakštaisnstūra augstums nav lielāks par 3	10
3.	$V <= 10$	17
4.	$N,M <= 300$	30
5.	Bez papildu ierobežojumiem	41

Apakšuzdevumu punktu summa = 100.

1. apakšuzdevuma ievaddati

6 7 3
1 2 3 -3 0 1
4 -5 3 5 -4 -5
2 3 2 2 -1 5
-4 -3 -3 -5 1 5
-2 -2 -5 5 5 -5
5 -1 -3 1 -3 -4
0 3 -2 2 -5 3
1 7 5 1
6 4 1 1
2 1 5 1

Svītraino paklāju summas

ļoti grūts

Uzdevums no Latvijas 38. (2024./2025. m.g.) informātikas olimpiādes (LIO) valsts kārtas; vecākajai (11.-12. klašu) grupai.

Stāsts

Valtera mājās ir zemāk redzamais paklājs, par kura rakstu varētu teikt, ka tas sastāv no "koncentriskiem rūtiņu taisnstūriem".

Skatoties uz paklāja rakstu, Valters ir izdomājis, ka šim paklāja rakstam līdzīgu šablonu varētu izmantot skaitļu tabulā, summējot tajā ierakstītos skaitļus noteiktā veidā.

sākumā $S=0$ ,
visus skaitļus, kas atrodas uz šī apakštaisnstūra ārējā kontūra, pieskaita $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, atņem no $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, pieskaita $S$ ,
tad visus skaitļus, kas atrodas uz nākamā kontūra, atņem no $S$ ,
utt., pārmaiņus skaitļus no kārtējā kontūra vai nu pieskaita, vai atņem no $S$ .

Uzrakstiet datorprogrammu, kas dotam laukuma rūtiņu aizpildījumam un apakštaisnstūru novietojuma aprakstam katram no apakštaisnstūriem aprēķina svītrainā paklāja summu!

Ievaddati

Pirmajā rindā doti trīs naturāli skaitļi - rūtiņu laukuma platums $N$ ( $N \leq 1000$ ), laukuma augstums $M$ ( $M \leq 1000$ ) un vaicājumu skaits $V$ ( $V \leq 2 \cdot 10^5$ ).

Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.

Izvaddati

Piemēri

Ievaddati

10 8 4
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
7 5 4 3
8 8 3 1
1 2 5 5
1 1 4 2

Izvaddati

Piezīme:

Atbilst piemēram uzdevuma tekstā.

Ievaddati

10 8 4
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
7 2 4 3
1 5 7 2
1 1 6 5
10 8 1 1

Izvaddati

Izpildes resursu ierobežojumi

CPU izpildes laiks uz testu: 0.6 sekundes.

RAM atmiņas apjoms uz testu: 256 megabaiti.

Apakšuzdevumi un to vērtēšana

#	Apakšuzdevuma apraksts	Punkti
1.	Uzdevuma tekstā dotais tests	2
2.	Visos vaicājumos apakštaisnstūra augstums nav lielāks par 3	10
3.	$V <= 10$	17
4.	$N,M <= 300$	30
5.	Bez papildu ierobežojumiem	41

Apakšuzdevumu punktu summa = 100.

1. apakšuzdevuma ievaddati

6 7 3
1 2 3 -3 0 1
4 -5 3 5 -4 -5
2 3 2 2 -1 5
-4 -3 -3 -5 1 5
-2 -2 -5 5 5 -5
5 -1 -3 1 -3 -4
0 3 -2 2 -5 3
1 7 5 1
6 4 1 1
2 1 5 1