
Seifs

Stāsts
Inženieris Žeņa veido izsmalcinātu elektroniski-mehānisku seifa atslēgu, kura sastāv no apļveida korpusa ar kontaktiem un grozāma koncentriska regulāra -stūra tā iekšpusē. Katra daudzstūra virsotne arī ir kontakts. Sākotnēji katra regulārā daudzstūra virsotne atrodas pretī kādam no korpusa kontaktiem. Iekšējais daudzstūris ir grozāms, bet tikai par konstantu soli - veselu skaitu iedaļu. Tādējādi, iekšējā daudzstūra virsotnes arī pēc pagriešanas vienmēr atrodas pretī korpusa kontaktiem. Vienam vai vairākiem korpusa kontaktiem ir pievienoti sarkani vadi, kas tos savieno ar citām elektroniskās shēmas sastāvdaļām. Līdzīgi, daudzstūra iekšpusē esošās komponentes ir savienotas ar daudzstūra virsotnēm, izmantojot zilus vadus.
Gan korpusa, gan daudzstūra virsotņu kontakti ir numurēti pulksteņrādītāja virzienā ar naturāliem skaitļiem no līdz pēc kārtas. Sākotnēji katram , kontakti ar vienādiem numuriem ir savienoti (atrodas pretī viens otram).
Nepieciešams pēc iespējas mazāku pagriezienu skaitu pulksteņrādītāja virzienā pagriezt iekšējo daudzstūri tā, ka nevienam savienoto kontaktu pārim abiem nebūtu pievienoti vadi. Vai arī noteikt, ka to izdarīt nevar.
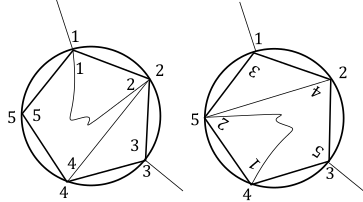
Piemēram, ja un vadi pievienoti korpusa kontaktiem un , kā arī daudzstūra virsotnēm , un (skat. attēlu), tad daudzstūri pagriežot par trim iedaļām, tiks panākts, ka nevienam savienoto kontaktu pārim abiem vienlaicīgi vadi nav pievienoti. Daudzstūra virsotnes ar pievienotiem vadiem tagad atrodas pret korpusa kontaktiem , un .
Uzrakstiet datorprogrammu, kas nosaka mazāko iedaļu skaitu, par kādu pulksteņrādītāja virzienā jāpagriež iekšējais daudzstūris, lai nevienam savienoto kontaktu pārim nebūtu pievienoti abi vadi, vai arī, ka šāds pagrieziens neeksistē!
Ievaddati
Ievaddatu pirmajā rindā dots naturāls skaitlis - iedaļu skaits .
Otrajā rindā dots to korpusa kontaktu, kuriem pievienoti vadi, apraksts: pirmais ir vesels nenegatīvs skaitlis - šādu kontaktu skaits, kam augošā secībā seko naturāli skaitļi robežās no līdz - šo kontaktu numuri.
Trešajā rindā tādā pat formātā ir aprakstīti daudzstūra virsotņu kontakti, kam ir pievienoti vadi.
Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada vesels skaitlis - mazākais iedaļu skaits, pa kādu pulksteņrādītāja virzienā jāpagriež iekšējais daudzstūris, lai iegūtu uzdevuma tekstā aprakstīto situāciju, vai , ja tādu panākt nav iespējams.
Piemēri
Ievaddati
5
2 1 3
3 1 2 4
Izvaddati
3
Ievaddati
7
6 1 2 4 5 6 7
2 3 5
Izvaddati
-1
Ievaddati
6
0
3 2 4 6
Izvaddati
0
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma tekstā dotie trīs testi. | 2 |
| 2. | . | 28 |
| 3. | . | 30 |
| 4. | Bez papildu ierobežojumiem. | 40 |
1. apakšuzdevuma ievaddati
10
3 1 8 10
5 2 3 4 7 8
20
5 1 8 16 17 18
6 1 2 3 6 16 19

Seifs

Stāsts
Inženieris Žeņa veido izsmalcinātu elektroniski-mehānisku seifa atslēgu, kura sastāv no apļveida korpusa ar kontaktiem un grozāma koncentriska regulāra -stūra tā iekšpusē. Katra daudzstūra virsotne arī ir kontakts. Sākotnēji katra regulārā daudzstūra virsotne atrodas pretī kādam no korpusa kontaktiem. Iekšējais daudzstūris ir grozāms, bet tikai par konstantu soli - veselu skaitu iedaļu. Tādējādi, iekšējā daudzstūra virsotnes arī pēc pagriešanas vienmēr atrodas pretī korpusa kontaktiem. Vienam vai vairākiem korpusa kontaktiem ir pievienoti sarkani vadi, kas tos savieno ar citām elektroniskās shēmas sastāvdaļām. Līdzīgi, daudzstūra iekšpusē esošās komponentes ir savienotas ar daudzstūra virsotnēm, izmantojot zilus vadus.
Gan korpusa, gan daudzstūra virsotņu kontakti ir numurēti pulksteņrādītāja virzienā ar naturāliem skaitļiem no līdz pēc kārtas. Sākotnēji katram , kontakti ar vienādiem numuriem ir savienoti (atrodas pretī viens otram).
Nepieciešams pēc iespējas mazāku pagriezienu skaitu pulksteņrādītāja virzienā pagriezt iekšējo daudzstūri tā, ka nevienam savienoto kontaktu pārim abiem nebūtu pievienoti vadi. Vai arī noteikt, ka to izdarīt nevar.

Piemēram, ja un vadi pievienoti korpusa kontaktiem un , kā arī daudzstūra virsotnēm , un (skat. attēlu), tad daudzstūri pagriežot par trim iedaļām, tiks panākts, ka nevienam savienoto kontaktu pārim abiem vienlaicīgi vadi nav pievienoti. Daudzstūra virsotnes ar pievienotiem vadiem tagad atrodas pret korpusa kontaktiem , un .
Uzrakstiet datorprogrammu, kas nosaka mazāko iedaļu skaitu, par kādu pulksteņrādītāja virzienā jāpagriež iekšējais daudzstūris, lai nevienam savienoto kontaktu pārim nebūtu pievienoti abi vadi, vai arī, ka šāds pagrieziens neeksistē!
Ievaddati
Ievaddatu pirmajā rindā dots naturāls skaitlis - iedaļu skaits .
Otrajā rindā dots to korpusa kontaktu, kuriem pievienoti vadi, apraksts: pirmais ir vesels nenegatīvs skaitlis - šādu kontaktu skaits, kam augošā secībā seko naturāli skaitļi robežās no līdz - šo kontaktu numuri.
Trešajā rindā tādā pat formātā ir aprakstīti daudzstūra virsotņu kontakti, kam ir pievienoti vadi.
Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumzīme.
Izvaddati
Izvaddatu vienīgajā rindā jāizvada vesels skaitlis - mazākais iedaļu skaits, pa kādu pulksteņrādītāja virzienā jāpagriež iekšējais daudzstūris, lai iegūtu uzdevuma tekstā aprakstīto situāciju, vai , ja tādu panākt nav iespējams.
Piemēri
Ievaddati
5
2 1 3
3 1 2 4
Izvaddati
3
Ievaddati
7
6 1 2 4 5 6 7
2 3 5
Izvaddati
-1
Ievaddati
6
0
3 2 4 6
Izvaddati
0
Izpildes resursu ierobežojumi
Apakšuzdevumi un to vērtēšana
| # | Apakšuzdevuma apraksts | Punkti |
|---|---|---|
| 1. | Uzdevuma tekstā dotie trīs testi. | 2 |
| 2. | . | 28 |
| 3. | . | 30 |
| 4. | Bez papildu ierobežojumiem. | 40 |
1. apakšuzdevuma ievaddati
10
3 1 8 10
5 2 3 4 7 8
20
5 1 8 16 17 18
6 1 2 3 6 16 19